Next: About this document ...
|
Obłok materii międzygwiazdowej
- zapadanie wskutek samograwitacji, jeśli spełnia warunek Jeansa - dzielenie się na wiele obłoków i tworzą się pojedyńcze gwiazdy ( - może utworzyć układ planetarny (znamy ponad 100 układów) |
![]()
| Brązowy karzeł | Gwiazda ciągu głównego(karzeł) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| - nigdy nie zapłoną reakcje | - najdłuższy okres z życia gwiazdy | |||||||||||||
| - powoli gaśnie | - czas życia:
|
|||||||||||||
| - gwiazda od rozpoczęcia reakcji jądrowych (spalanie wodoru w hel) | ||||||||||||||
|
||||||||||||||
|
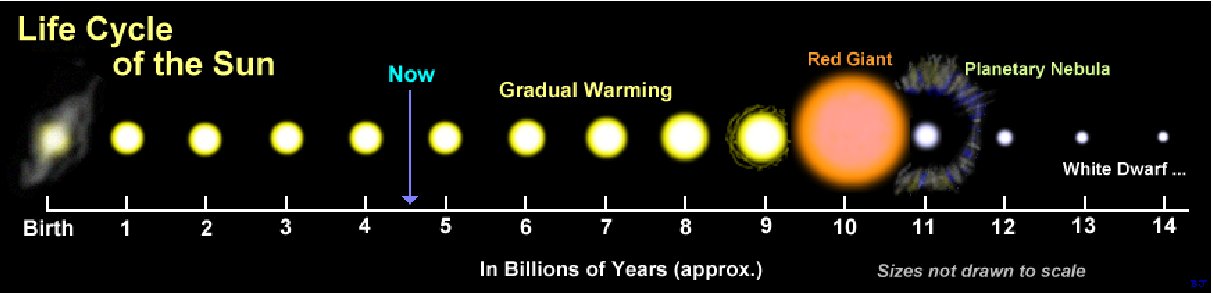
- Słońce: 86% energii z cyklu p-p, łącznie spala |
||||||||||||||
| - energia grawitacyjna Słońca starczyłaby na |
||||||||||||||
| - najbardziej stabilny okres, stała moc promieniowania |
![]()
| Czerwony karzeł | Czerwony olbrzym(lub nadolbrzym) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| - czas spalania>wiek Wszechświata | - wypalenie wodoru w jądrze, kurczenie się gwiazdy (palenie wodoru w otoczce) aż do zapłonięcia helu (reakcja 3 |
||||||||||
| - sądzimy, że b.wolno | - rozszerzenie się gwiazdy ok.100 razy | ||||||||||
| gasną | - jak się w jądrze skończy hel to kolejne reakcje (do którego pierwiastka | ||||||||||
| dojdzie zależy od masy gwiazdy), najdalej może powstać jądro żelazne (dalej synteza wymaga dodatkowej energii) | |||||||||||
r0.39
|
| - powolne odrzucanie | Supernowa typu II | |||||||||||
| materii i zapadanie się | - koniec reakcji w jądrze (nagle próżnia) i kolaps w ułamku sekundy po czym wybuch | |||||||||||
|
|
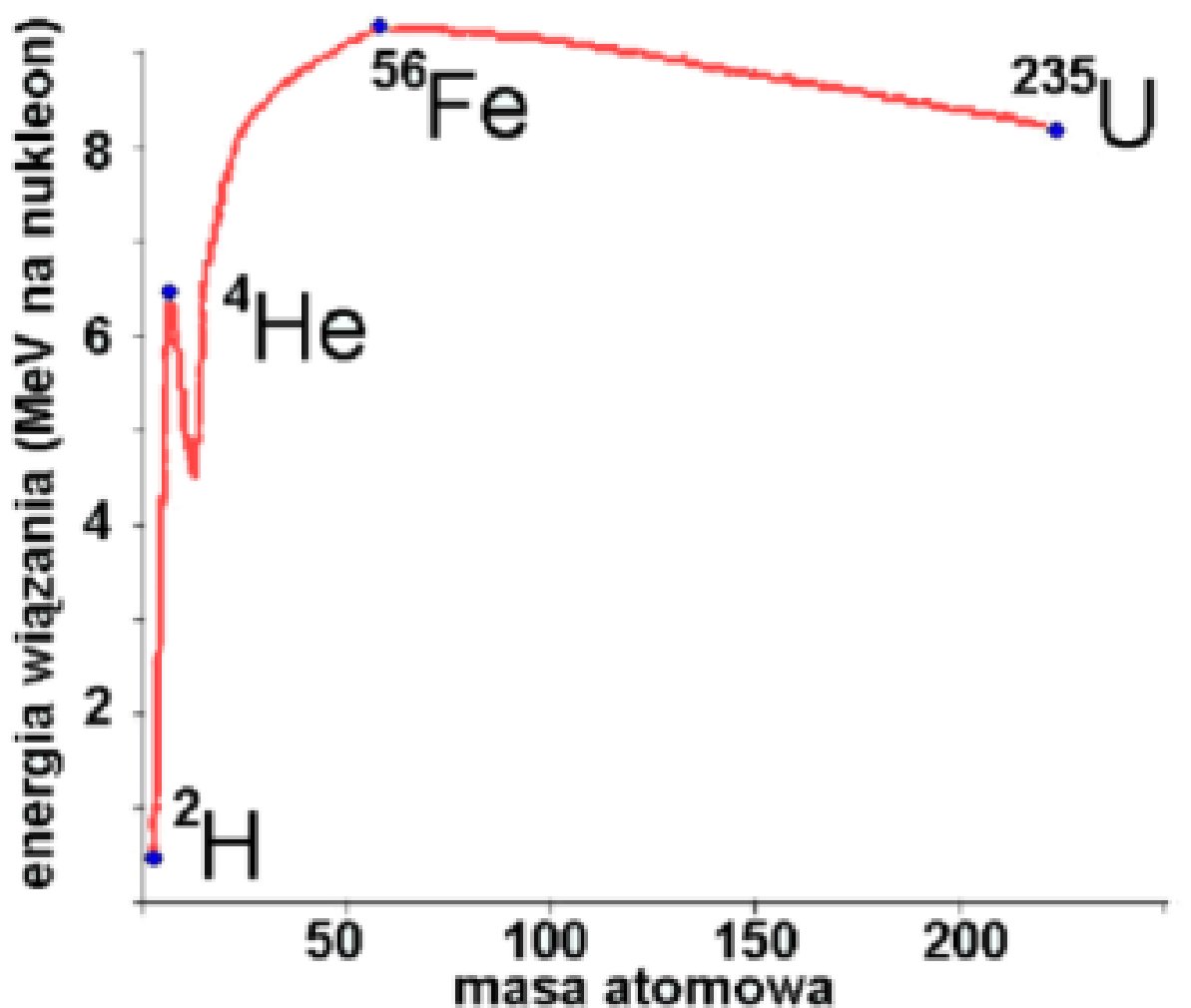
- takie energie, że powstają pierwiastki cięższe od żelaza (od Fe do U), | |||||||||||
| Mgławica Planetarna | jedyny znany nam taki proces w przyrodzie | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| - odrzucona materia | - w Galaktyce zanotowano 6 wybuchów (ostatni 1604r. przez Keplera) | |||||||||||
| - wyrzucenie od 0.1 do 0.9 masy gwiazdy | ||||||||||||
|
|
|
|||||||||||
| Biały karzeł | Pozostałość po supernowej | |||||||||||
| - odrzucona w wybuchu materia | ||||||||||||
|
Późne etapy ewolucji gwiazd:
| Biały karzeł | Gwiazda neutronowa | Czarna dziura |
|---|---|---|
| - masy
|
- zbudowane głównie z neutronów | - nic nie zatrzyma grawitacji i zapadanie się aż |
| - promienie
|
(ogromne ciśnienie stąd reakcje | do tzw.. osobliwości (kwantowa grawitacja) |
| -
|
|
- masy od |
|
|
- promienie |
- nie ma fizycznego promienia, tylko promień |
| - masy rzędu |
horyzontu zdarzeń (prędkość ucieczki = c) | |
| - gaz zdegenerowany | (ogólnie |
promień Schwarzschilda
|
|
|
- gęstość w centrum
|
- Przykłady: Dla
|
| - silne pole mag. |
|
|
| (Ziemia |
- obserwujemy ich działanie na otaczającą | |
| - szybka rotacja, okresy rzędu sekund | materię | |
| PULSARY | ||
| - wysyłają silny strumień elektronów, | Inne czarne dziury: centra galaktyk | |
| jak Ziemia na drodze stożka to | (masy rzędu
|
|
| "widzimy" pulsy | Część bardzo aktywna (np. kwazary) | |
| - najsłynniejszy: Mgławica Krab | - energie 10 tys. razy przeciętna galaktyka | |
| (wybuch 1054r., |
- rozmiary rzędu 20 AU | |
| - był widoczny bez teleskopów przez: za dnia (23 dni), w nocy (2 lata) | ||
| - znane są 2 posiadające planety | ||
![\includegraphics[width=5cm, height=4.5cm, bb=14 14 873 900]{pulsar.eps}](img48.png)
|
|
M( |
Formowanie | Ciąg główny | Faza olbrzyma |
| 1 | |
|
|
| 5 | |
|
|
| 10 | |
|
Ewolucja na diagramie HR:
|
Twinkle Twinkle little star, I don't wonder what you are; For by spectroscopic ken, I know that you're hydrogen; |