Definiuje się parametr gęstości:
Oznaczamy:
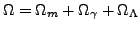
Wtedy 1 równanie Friedmanna:
Oszacowanie wartości w chwili teraz:
- dla większych wartości Wszechświat by dawno skolapsował
- dla mniejszych wartości Wszechświat by dawno skolapsował
- większe byśmy ją łatwo dostrzegli
Wynika to z:
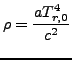 , gdzie
, gdzie
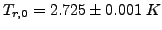 i
i
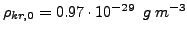 .
.
Zatem OBECNIE zaniedbywalne.
Dokładne wartości np. z konkretnego modelu kosmologicznego i porównaniu go do naszego Wszechświata:
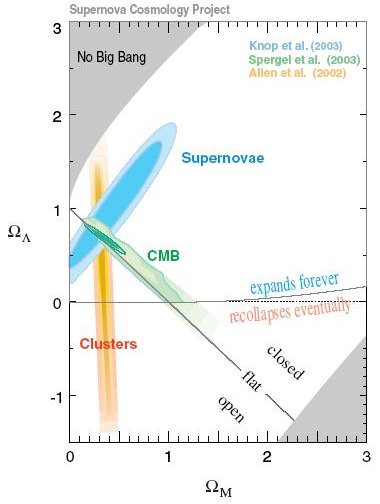
Rysunek:
Model Wszechświata pokazujący ograniczenia na parametry gęstości z obserwacji (i powstałych na ich podstawie modeli) CMB (ang. Cosmic Microwave Background, kosmicznego promieniowania tła), gromad galaktyk i supernowych
|
|
Stąd dostajemy wartości:
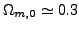
i
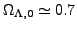
Bogna Pazderska
2008-03-30
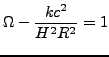
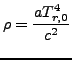 , gdzie
, gdzie