Next: Gęstość krytyczna Up: Podstawy kosmologii Previous: Podstawy kosmologii
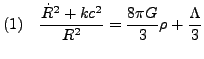
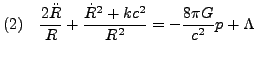
![]() - gęstość (suma gęstości 3 składników:
- gęstość (suma gęstości 3 składników: ![]() ,
, ![]() i
i ![]() )
)
p - ciśnienie (suma ciśnień 3 składników: ![]() ,
, ![]() i
i ![]() )
)
k - wybór metryki (rodzaj krzywizny przestrzeni)
Możliwe krzywizny:
Klasycznie (bez stałej kosmologicznej i dla k = 0) można je wyprowadzić z:
1. Tw. Birkhoffa z OTW (prędkość V zależy od tego co się dzieje wewnątrz sfery o promieniu R o centrum w obserwatorze) w zastosowaniu do zasady zachowania energii
2. I zasada termodynamiki
Bogna Pazderska 2008-03-30