a) redshift (poczerwienienie):
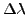 - zmiana długości fali w widmie
- zmiana długości fali w widmie
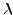 - długość laboratoryjna danego pierwiastka/molekuły
- długość laboratoryjna danego pierwiastka/molekuły
b) t - czas kosmiczny (tzw. perspektywa Boga)
c) odległość własna (odległość do obiektu), zał. zaniedbujemy ruchy własne ciał:
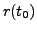 - odległość w chwili teraz
- odległość w chwili teraz
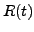 - czynnik skali (konkretny model kosmologiczny = postać matematyczna tego czynnika)
- czynnik skali (konkretny model kosmologiczny = postać matematyczna tego czynnika)
Rysunek:
Zmiana skali Wszechświata przy izotropowym rozszerzaniu (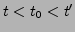 )
)
|
|
Związek z redshiftem:
d) parametr Hubble'a:
e) stała Hubble'a:
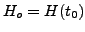 - parametr Hubble'a w chwili teraz
- parametr Hubble'a w chwili teraz
Wartość (bliskie odległości - setki Mpc):
Albo:
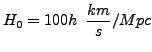 , gdzie h=0.72
, gdzie h=0.72
(
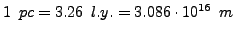 )
)
Jest to stała w sensie współczynnika proporcjonalności i w sensie stałości względem kierunku - przynajmniej tak wynika z obserwacji.
Bogna Pazderska
2008-03-30
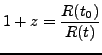
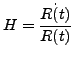
![]() - parametr Hubble'a w chwili teraz
- parametr Hubble'a w chwili teraz
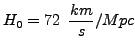
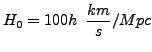 , gdzie h=0.72
, gdzie h=0.72